CS46B Lab 13 - Trees

Copyright © Cay S. Horstmann 2012
This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 United States License.

A. Binary Trees

Write down (using ASCII art) all possible binary tree shapes of trees with 1 node, 2 nodes, and 3 nodes. (There are 1, 2, and 5 shapes respectively).
Now consider a binary tree with n nodes. The root has children t1 and t2. Suppose t1 has k nodes. How many nodes does t2 have?
Now we want to write a recursive formula for the number S(n) of tree shapes with n nodes. For each k = 0 ... n - 1, there are S(k) x S(?) possibilities, since you can indepently choose the shape of the left and right subtree. So, S(n) = S(0) x S(?) + S(1) x S(?) + ... + S(?) x S(?). Fill in the ?.
You also need base cases for S(0) and S(1). What are they?
Using this formula, compute S(2) and S(3). What values does the formula give? Are they the same that you got in part 1?
Complete this program and have it compute S(10) and S(20). What do you get? (Run it from the command line as java Trees1 10 and java Trees1 20.)
Why does the computation of S(20) take so long?
What one-line bash command can give you all results S(1), (2), ..., S(20)? (Hint: seq—see Lab 9.)

B. Random Trees

Now we want to make a random tree with n nodes. That's simpler than you might think. Randomly pick a k < n for the number of nodes of the left subtree. Generate random trees of size k and n - 1 - k. Combine them to a complete tree.
Complete this program. (You need the BinaryTree class from Chapter 17 Section 2.)

What is the code of your randomTree method?
Now run the program. What happens? Why?
Yes, we could write a toString method, and we will do that presently. But first, let's look at the tree in the debugger. Set a breakpoint at the last line of main and run the program. Get out a sheet of paper. Inspect t. Keep expanding the left and right nodes. From the display, sketch the tree, like you did in Lab 7.
Hand the sketch to the lab instructor.
Is that tree a binary search tree? Why or why not?
Now let's write a toString method. Ideally, we might like something like
```
           6
         /   \
        3     2
       / \     \
      1   1     1
```
but that's pretty hard to do in general. Instead, let's have a one-dimensional representation, something of the form
```
left subtree data right subtree
```
Let's do that. Add a method
```
public String toString()
```
to the BinaryTree class. It must call a recursive method on the root node. Let's call it toString as well:
```
public static String toString(Node n)
```
That's where the actual work gets done. (Look at height as another example of how this is done.)

In the Node.toString method, return a string as described above, with the left, data, and right separated by spaces. If the node is null, return ".".

What is your code?
Now run the program again. What output do you get?
That's still disappointing. We see the data in the tree, but we don't see the shape. An easy fix is to put a pair of parentheses around the tree.
```
(left subtree data right subtree)
```
Do this. What is your output now?
Suppose your output had been
```
((. 2 (. 1 .)) 6 ((. 1 .) 3 (. 1 .)))
```
Draw the correspnding tree.
What would be the string representation of the tree in step 5?

C. All Trees

For debugging a tree algorithm, we want to run it on all possible tree shapes. It's easy enough to generate a list of all trees of size n. For each k, generate all trees of size k and of size n - 1 - k in lists l1 and l2. Then, for each tree t1 in l1 and for each tree t2 in l2, make a tree with children t1 and t2,
```
for (BinaryTree t1 : l1)
{
   for (BinaryTree t2 : l2)
   {
       BinaryTree t = new BinaryTree(n, t1, t2);
      ...
   }
}
```
Put each tree in a list l and return it.

Complete the allTrees method in this class. What is your code?
Print all trees of size 6. What is your output?
Modify your program to print only those of height 6. Which ones are they?
How many are there? Why?
What is the smallest height that a tree of size 6 can have?
Modify your program to print only those trees. Which ones are they?
How many are there? (Hint: Don't count by hand—use wc, as shown in Lab 9.)

D. Binary Search Trees

We want to put our new powers to work by testing the deletion algorithm for binary search trees. (It seems tricky enough to be worth testing thoroughly.) The plan is to generate all binary search trees of a given size, then delete all possible elements, and verify each time that the result is correct.
Problem #1. The BinarySearchTree class in Chapter 17 Section 3 is different from the BinaryTree class that we used so far.

Why can't we just change BinaryTree to BinarySearchTree in Trees3?

Why doesn't the BinarySearchTree have a constructor

public BinarySearchTree(Object rootData, BinarySearchTree left, BinarySearchTree right)

The easiest way to move forward is to remove the private from
```
private Node root;
```
in BinarySearchTree. Now root (and the Node class) are package-visible. When we add a class Trees4 to the default package, it can access the root field.

Next, declare the Node class as static:
```
static class Node
```
This is a very technical detail—it means that a Node can be constructed outside a BinarySearchTree.

For example, suppose you have trees t1 and t2, and now you want to make a new tree with both of them, you can use this brute-force code:
```
BinarySearchTree t = new BinarySearchTree();
t.root = new BinarySearchTree.Node();
t.root.left = t1.root;
t.root.right = t2.root;
```
Not very object-oriented, but it's ok for a test harness that is meant to test the internals of the implementation.

Using this technique, make a copy of Trees3, call it Trees4, change all BinaryTree to BinarySearchTree, and construct the trees as described above. Also set t.root.data = n in the second and third branch; e.g.
```
for (BinarySearchTree t1 : l1)
{
   for (BinarySearchTree t2 : l2)
   {
      BinarySearchTree t = new BinarySearchTree();
      t.root = new BinarySearchTree.Node();
      t.root.data = n;
      ...
   }
}
```
What does your program print? Why?
Add the toString to the BinarySearchTree class. In toString, you can't just use print. Why?
Instead, add toString in the same way as you did before. Now what does your program print?
Problem #2. These trees are not binary search trees. Let's write a method that takes a tree and fixes it up to be a binary search tree. For testing the algorithms, it doesn't matter much what the node data are, so we'll just set them to 1...n.
Here is our problem. We have a tree like
```
           *
         /   \
        *     *
       / \     \
      *   *     *
```
and now we want to fill in the data
```
           4
         /   \
        2     5
       / \     \
      1   3     6
```
Here is a recursive way of doing it. Look at the root. Fill in the left subtree, starting with 1, and have the recursive call tell you the next number to be used (4 in the example). Then fill in the root with the that data. Then fill in the right subtree starting with the next value (here 5). And ask it what its next number is (7). Return that number to the caller.

In Trees4, Implement a method
```
public static int fill(BinarySearchTree.Node n, int start)
```
that uses this strategy. What is your code?
Now add the loop
```
fill(t.root, 1);               
```
in main. What is your printout?

E. Deep Copying

Change the main method to

public static void main(String[] args)
{
   List<BinarySearchTree> trees = allTrees(6);
   int k = 1;
   for (BinarySearchTree t : trees)
   {
      fill(t.root, k);               
      k++;
   }
   for (BinarySearchTree t : trees)
   {
      System.out.println(t);
   }      
}

What values to you expect to have in the first tree? The second tree? The kth tree?

Run the program. Which is the first tree whose values are not correct?
Do you know why? If you have no idea, it's ok to say so.
Generally, when you have unexpected mutations in a data structure with nodes, it is because you have two references pointing to the same node, and both of them mutate the shared node.

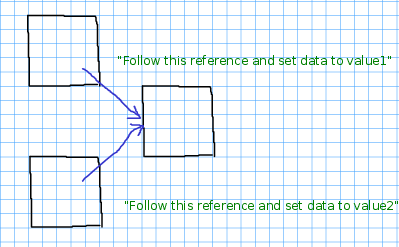
Then the second mutation overwrites the first.

Let's see if we have shared nodes in our trees.

When you make a new Node, you get a fresh, new one. Where does that happen in allTrees?
When you copy a node, like
```
a.left = n;
```
then both a.left and n point to the same node. Where does that happen in allTrees?
This sharing isn't a problem when your program doesn't mutate the data structure. (In fact, this is commonly done when you want to safely access data structures in parallel.) But it doesn't work for us—the remove method, which we want to test, mutates the tree on which it operates.
So, we need to make a copy of each tree.

Copying a tree seems generally useful, so let's add a method
```
public BinarySearchTree copy()
```
to the BinarySearchTree class.

How do you copy a tree? You construct a new root node and populate it with copies of the left and right subtrees. That's best done in a recursive method
```
public Node copy(Node n)
{
   if (n == null) return null;
   else
   {
      Node newRoot = ...;
      ...
      ...
      ...
      return newRoot;
   }
}
```
Add the copy methods to the BinarySearchTree class. What are your complete methods?
To test, change the line
```
System.out.println(t);
```
in Trees4 to
```
System.out.println(t.copy());
```
If you did everything right, you should get the same output.
Of course, that didn't fix our problem—we copied too late. Where do you need to copy?
Do that, and check the output. Is it now correct?

F. Finally—Testing Remove

Now we have all the parts ready for testing the remove method. Here's the plan. For a given n,
- Generate all tree shapes
- For each tree shape
  - Fill it with the numbers 1...n
  - For eack number k between 1 and n
  - - Make a copy
    - Remove k from the copy
    - Verify that the copy contains 1 ... n but not k
Add a JUnit class RemoveTest to your NetBeans project. What did you do to do that?
Add a method to the RemoveTest class
```
public void testRemove(int n)
```
Do just what the pseudocode did. Call Trees4.allTrees, Trees4.fill, find (in the BinarySearchTree), assertTrue, and assertFalse (from JUnit).

What is your method?
Now run the JUnit test. What happens?
That's because JUnit wants you to annotate test methods with @Test. What happens if you add @Test to public void testRemove(int n)?
That's because JUnit wants test methods to have no parameters. Remove that @Test and add
```
@Test public void testRemove6()
{
   testRemove(6);
}
```
What happens?
That's great, but of course we knew that the remove method worked. Just to see what happens when there is an error, locate the if statement
```
if (toBeRemoved.left == null) 
{
   newChild = toBeRemoved.right;
}
```
in BinarySearchTree.remove and inside the body, change right to left. Run the test again. What happens?

G. Reimplementing Remove

Now that we have a test that can tell us whether we are doing it right, let's reimplement the remove method. When you look at section 17.3.3 of your textbook, you will notice that the case “Removing a node with two children” makes an arbitrary choice. The node to be removed is replaced with the smallest value in the right subtree, when it could equally well be replaced with the largest value in the left subtree.
Consider this BST:
```
          2
        /   \
      1       7
           /     \
         4         11
        / \        /  \
       3   5     10    12
            \    /
             6  8
                 \
                  9
```
We want to remove 7.

How does the removal unfold, as described in the book?
How would the removal unfold if you implemented it in the alternate way, replacing 7 with the largest value in the left subtree?
Now change the remove method to do that. List all the changes that you had made.
Run the test. Did it pass?
If it didn't, what mistake(s) did you make?