CS46B Lab

Copyright © Cay S. Horstmann 2012
This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 United States License.

Objectives

Gain experience with the big-Oh notation
Measure the growth rate of the execution time of a program as input size varies

Learning Outcomes

Produce big-Oh estimates of simple algorithms
Analyze execution time measurements
Use Unix tools to extract data

A. Execution Timing

You know that removing an element from an array list of size n is O(n), and that's bad. Let's see how bad. Here is a simple program that adds elements 1...n to an array list and then removes them in opposite order. In a command shell, run
```
javac Remove1.java
java Remove1 1000
java Remove1 10000
java Remove1 100000
java Remove1 1000000
```
The command above work because I have my prompt point to my working folder. For example, my "Desktop" folder to which I put my Remove1.java. If your prompt is pointing somewhere else, you should provide an absolute path in the first command; plus, you must provide classpath option for the other 3 commands.
What do you notice?

It gets pretty slow. How slow? Pick a number at which the program run seems to take a second or two—noticeable but not yet painful. On my computer, that's 100000. On yours, it might be 70000 or 150000. Then run

time java Remove1 100000
time java Remove1 200000
time java Remove1 300000
time java Remove1 400000

Adjust the values as needed. For example, if you start with 70000, use 140000, 210000, 280000 for the other runs. What (user) times do you get? Make a table

n₁	t₁
n₂	t₂
n₃	t₃
n₄	t₄

where n_k is the number for the k^th run, and t_k is the time.

The absolute numbers aren't all that instructive. They depend on your computer speed. Divide by the first one to get the growth behavior:

n₁/n₁	t₁/t₁
n₂/n₁	t₂/t₁
n₃/n₁	t₃/t₁
n₄/n₁	t₄/t₁

What values do you get?

When you plot these values, what is the shape of the curve?
Huh? Removal is O(n), not O(n²). Why do you get that shape? (Hint: Read the code.)
Now change the ArrayList to a LinkedList. How do you expect the timing data to change? Why?
Repeat the measurements. What timing ratios do you get now? (You may need to start with a larger n₁.)

B. Computing the Median

You may have heard about the median house price—half the houses on the market sell for more, half for less. If you have houses selling for
$418K $439K $338K $410K $389K $405K $398K $388K $404K

what is the median?
Here is one way to compute the median. Compute the largest element. Compute the smallest element. Remove both of them.
Repeat until there are ≤2 elements. If there are two left, compute their average.

Look into the API documentation of the Collections class. What library methods can you use for computing the maximum and minimum?

Look into the API documentation of the List class. What library method can you use for removing a value (not an index)?
Complete this program. What is your code?
Run it:
```
javac Median1.java
java Median1 10000
```
What value do you get?
Why is that reasonable?
What execution times do you get for n = 10000 and n = 100000?
If you think about it, it's not actually necessary to remove the elements? Suppose we knew where the largest and smallest value are, instead of what they are. Then we could just fill in the last two elements of the array into those positions. Removing the last two elements is O(1), not O(n), so that's got to be a win.
Unfortunately, there is no library method for getting that position. Modify the algorithm in Section 6.7.5 of your textbook to get you the position of the largest value. What is the pseudocode?
You can compute the smallest position in the same loop. Fill in this program. What is your code?
What execution times do you get for n = 10000 and n = 100000?
That's a little better, but probably not dramatically so. What is the big-Oh efficiency of this algorithm? Why?

C. A Small Problem

Do this section if you have time. If not, go to D.

Actually, there is a small problem with the algorithm in Median2. You won't notice it with these random numbers, but it would be a problem with actual values. When smallestIndex or largestIndex is one of the last two positions in the array, then the smallest or largest element may not be removed. Find a situation where this happens in the first pass of the algorithm (with a short array). What is your array contents?
What should happen? What actually happens?
Now modify your example so that the actual median gets wrongly removed in that step, so you can write a unit test that shows the problem. What is your example?
Write that unit test. What is your code?
Run it. Does it really fail? If not, fix up your example until it does.
How do you fix the error? Pseudocode first.
Implement your fix. What is the code?
What happens when you run the unit test again?

D. Sorting

If the array is sorted, then it's much easier to compute the median. How? Consider both the case of an array of even length and of odd length.
Which method in the Collections class can you use to sort the array?
Implement that. What is your code?
What execution times do you get for n = 10000 and n = 100000?
What is the big-Oh efficiency of this algorithm? Why?

E. Finding the Median Without Sorting

It seems a shame to sort an array when all you care about is the middle element. There is a better way, using the partitioning step of the QuickSort algorithm (Special Topic 14.3).
For simplicity, let's assume here that the array has odd length.

For example, the sequence

5 3 2 6 4 1 1 3 7

is partitioned, using the head element as the pivot, yielding the elements ≤ 5 and > 5, in some order.

3 3 2 1 4 1 | 6 5 7

In which part is the median? The first or the second? Why?

Note that we don't ever half to look at the other half again. That's the win over sorting, which would have to sort both halves.
Ok, that wasn't rocket science. Now if the first half was sorted, in which position would the median be?
It's no longer the middle element, so we can't recursively find the median of the chosen half. But it's just as easy to solve the slightly more general problem, to pick the kth element. This is usually called select(k).
In a sorted array, what is the big-Oh efficiency of select(k)?
Ok, that wasn't rocket science (hopefully). But we want to compute select(k) without sorting. In step 1, you saw that you can recursively call select(k) on the first part when the first part has at least k elements. Time for a helper method:
```
select(k, 0, n - 1) = select(k, 0, p) if p = partition(0, n - 1) and k <= p
```
But it could equally well happen that the first part has < k elements. Then the kth element must be in the second half. But it won't be the kth element!

Construct an example where that happens—nine elements, where more than half are larger than the first. What is the initial sequence? What is the partitioned sequence?
What is the median element (i.e. k = 4)? If the second half was sorted, where would it be?
Fill in:
```
select(k, 0, n - 1) = select(..., p + 1, n - 1) if p = partition(0, n - 1) and k > p
```
When can the recursion stop?
Fill in Median3.java. What is your select method? Note that this isn't quite so simple because from need not be zero.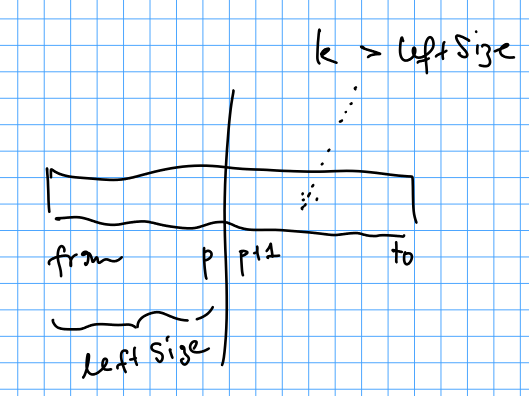
What execution times do you get for n = 10001 and n = 100001?
What is the big-Oh efficiency of this algorithm, assuming that the partition cuts the array approximately in half with every step? Why?
That assumption isn't going to be fulfilled for all arrays. In particular, what will happen if the array is already sorted?
What is the big-Oh efficiency in that case?

Change

      for (int i = 1; i <= n; i++) lst.add(Math.random());

      for (int i = 1; i <= n; i++) lst.add(i * 1.0);

What execution times do you get now?

F. Select2

Do this section if you have time.

What if the array had even length? Then the median would be the average of select(n/2) and select(n/2 + 1). But it seems a shame to run the algorithm twice when it is going to do essentially the same work twice over.
Develop a recursive select2(k, from, to) that returns an array of size 2 holding the kth and (k+1)st element. What is your pseudocode?
Come up with a JUnit test for select2. What is it?
Implement select2. What is your implementation?
What happens when you run the unit test?
Come up with a JUnit test for median with an even length array. What is it?
Implement median to call select2 if the array has even length. What is your code?
What happens when you run the unit test?
What is the change to the big-Oh efficiency?

G. Another Small Problem (Maybe)

Do this section if you have time.

Have another look at the quicksort implementation:
```
      int p = partition(from, to);
      sort(from, p);
      sort(p + 1, to);
```
What bad thing would happen if partition(from, to) returned to?
Actually, this is a bit subtle. When the interval has length 1, then partition will return to, and that's ok. Why?
Ok, can it happen that from < to and partition(from, to) returns to? Let's look at some simple cases. Walk through an array with elements
```
1 2 3 4 5 6
```
Walk through the call partition(0, 5). Make a walkthrough table that shows how i and j change. What is your table?
What is returned?
Ok, that didn't return to. Repeat for the array
```
6 5 4 3 2 1
```
That didn't return to either. What if all the elements are the same?
```
1 1 1 1 1 1
```

It's time to approach this systematically. Have a look at the outer loop in the partition method:

   private int partition(int from, int to)
   {
      int pivot = a[from];
      int i = from - 1;
      int j = to + 1;
      while (i < j)
      {
         i++; while (a[i] < pivot) i++;
         j--; while (a[j] > pivot) j--;
         if (i < j) swap(i, j); 
      }
      return j;
   }

How do you know that it must be entered at least once? (Remember the assumption that from < to).

Consider how j changes after the first traversal. The only way that j can equal to is if the loop
```
while (a[j] > pivot) j--;
```
is never entered. Why?
Ok, that's the case with an array of the form
u ? ? ? ? ? v

where u ≤ v. What is the contents of the array after the first iteration of the loop?
What are i and j after the first iteration of the loop?
How do you know that the loop must be entered a second time?
What happens to j in that second iteration?
Why does that solve our problem?