CS46B Lab 5

Copyright © Cay S. Horstmann 2010 - 2015
This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 United States License.

Modified by:

Thong Nguyen
Kathleen O'Brien

Instructions

Working in Pairs

You work in pairs
One of you is the “scribe”, the other the “driver” who runs the tools
The scribe answers the questions, except for the questions that say "paste the code"—the driver does the pasting.
Next week, you switch roles
Scribe: Start writing a report with the title “Scribe's name (Scribe) / driver's name (Driver)”, for example Lab 1 Fred Foo (Scribe) / Becky Bar (Driver)
Driver: Start writing a report with the title “Driver's name (Driver) / scribe's name (Scribe)”, for example Lab 1 Becky Bar (Driver) / Fred Foo (Scribe)
When a step contains a question, the scribe puts the answer in the scribe report. Otherwise, just put “Step n: done”
When a step asks "what is your code", the driver pastes the code into the driver report.
Stuck? Discuss with your buddy, and if you are both stuck, ask for help!!! (In class only).
Read these lab rules

Objectives

Practice recursion
Use the debugger in complex situations: recursion
Use logging
Understand the advantages of logging over print statements

Learning Outcomes

Implement simple and complex recursions
Understand the behavior of the debugger when tracing recursive methods
Set conditional breakpoints
Use logging statements
Turn off logging in a working program

A. A Simple Recursion

Here is a class Maze that you can initialize with a maze such as 13 X 29

         *****************************
         ** ***                      *
         ** *** * ********************
         ** *** *         *          *
         ** *** * *******   **********
         **     * ********************
         ****** ******* ******* ******
         ******         ******* ******
         *      ******* ******* ******
         * **** ******* **           *
         *    * ******* ******* ******
         * **** ******* ***     ******
         ************** **************

The * are walls, and the blank spaces are corridors. Each corridor is one space wide (horizontally or vertically).

Given a row and column, how can you tell whether you are at an exit of a given maze? (Using the Maze class, of course.)

Here is a class Robot that lives in a maze. Make a project with these classes and this MazeSolver class.
Your job is to complete the recursive escape method so that the robot escapes the maze and prints the trail.

Start with the base case:
- If the robot is already at an exit, return.
What is the code of your escape method so far?
If the robot is not at an exit, it follows the “right hand rule”: Always have a wall to the right.

You may assume the robot has been placed with a wall to the right when it was constructed. Now go on:
- If you can't move forward, turn left.
(There is no point turning right? Why?)
- If you can move forward, do it.
You may have lost the wall to the right. Make a sketch (in ASCII art) showing how this can happen.
The robot can't see to the right. It can only see forward (with canMove). How can it check whether it has lost the wall (no wall to the right)?
If it has lost the wall (the block on the right is not a wall block ( * ) ), then have the robot turn right and move.
It must then again have a wall to the right. Why?
If it hasn't lost the wall (there is a wall to the right), turn back to the original position.
(You had to turn to see the wall.)

What is your code so far?
Now the robot is at a new position. Then call escape so that it can escape from that position. That's your recursion.
What is the complete code of your escape method?
What happens when you run the MazeSolver program?
It would be a good idea to scroll through all the output and be sure you understand why the robot moves as it does.
Ok, it was recursive, but how could you have easily written this program without recursion? Don't rewrite it, just tell me.

B. A More Complex Recursion

The right hand rule doesn't work if the maze has cycles—paths that lead back to the same spot. Sketch an example.

We'll use a more complex algorithm for this purpose. Make a second method called escape2:

Make the robot turn around in all four directions.

In each direction with a path emanating from it (i.e canMove is true), the robot clones itself. Move the clone into the path (one step), and let it escape (call escape2()).

Complete the loop:

public boolean escape2()
{
   if (atExit()) return true;
   for (int i = ...) // this loop makes the robot check all possible direction
   {
      turnRight();
      if (...)
      {
         Robot cloned = clone();
         cloned....();
         if (cloned.escape2())
         {
            visited...
            return true;
         }
      }
   }
   return false;
}

What is your code?

What happens when you run the program? Remember to change the call in the MazeSolver to escape2
This code will work for any maze.
Can you easily rewrite escape2 without recursion?
Why or why not?

C. Simulating Recursion

One way to visualize recursive calls is with index cards. Make one card per call. Write the values of all known values. When you come to the recursive call, write ? next to it and make another card.
Let's try it with this method:
```
int triangleArea(int width)
{
   if (width == 1) return 1;
   int smallerArea = triangleArea(width - 1);
   int area = smallerArea + width;
   return area;
}
```
Make an index card like this:
```
triangleArea(width = 4)
smallerArea = triangleArea(3) ?
```
Now put this one aside and make another one for the call to triangleArea(3). Put this one aside too, on the top of the preceding one.

Keep going:
```
triangleArea(width = 2)
smallerArea = triangleArea(1) ?
```
When you reach triangleArea(1), the card looks different:
```
triangleArea(width = 1)
return 1
```
Now find the card with the ? next to triangleArea(1). Cross out the ? and write the returned value 1 next to it. Now you can continue the method:
```
triangleArea(width = 2)
smallerArea = triangleArea(1) = 1
area = 1 + 2 = 3
return 3
```
Do you have a card calling for triangleArea(2)? It's got to be there somewhere. Cross out the ? and write 3 next to it. Keep on going.

This activity should give you an idea of the stack of method calls that are pending as the recursion progresses.

What do you get for triangleArea(4) when all is done?

Now let's do the same with a different method:

int largest(int[] values, int start, int res)
{
   if (start == values.length) return res;
   int res2 = Math.max(res, values[start]);
   return largest(values, start + 1, res2);
}

Let's study the call

largest(new int[] { 3, 4, 1 }, 0, Int.MIN_VALUE)

Make a card

largest(values = [3, 4, 1], start = 0, res = Int.MIN_VALUE)
res2 = ... 
return largest(values, ..., ...) ?

What did you fill in for the ...?

Note the ?. We don't know the answer, so make a new card. What is your card?
You'll need another card. What is it?

And another. This one is much simpler.

largest(values = [3, 4, 1], start = 3, res = ...)
return ...

What is ...?

Now unroll the recursion. What is the answer?
Why is it easier than with the triangle numbers?
You have just seen a “tail recursion”, in which the recursive call is the last item in the computation. These recursive calls can be automatically translated into loops, which gives you the best of both worlds—easy code and good performance.

D. Debugging Recursive Methods

The RecursiveFib class is from your text book.
Run the program with n = 50. What happens?

If you find it running too slowly, you can terminate it by clicking on the stop (red square) button of the console window.
When I tried this on a moderately fast laptop, the computation slowed down after
```
fib(42) = 267914296
fib(43) = 433494437
```
But that's weird. Given these two values, it is trivial to compute fib(44). What is it? (Get out a calculator. Calculate 267914296+433494437)
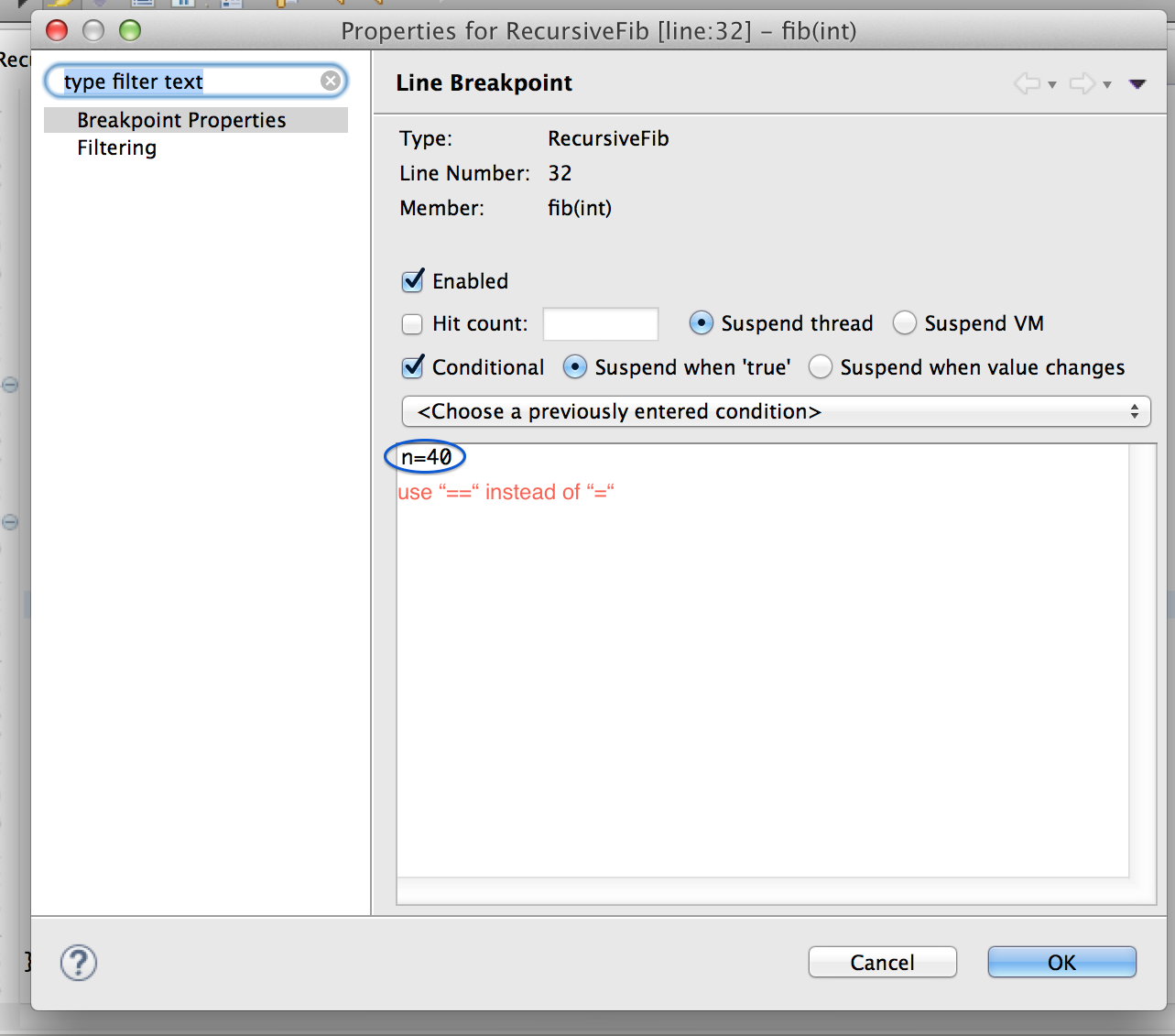
Now we want to trace into the fib method. Let's say we want to step through fib(40). But it is called in a loop. We don't want to click the "Step Over" button 40 times. That's where conditional breakpoints come in.
Make a breakpoint on line if (n <= 2). Right-click on it and select Breakpoint -> Properties. Click on “Break when hit count” and enter 40 after “equals to”.

Now select Run → Debug from the menu.

What happens?

If the program does not stop, you may not be in debug perspective. Look at the upper right. That shows thecurrent persective. If Debug is not selected, select it. Now try Run → Debug
Step into the fib method. Keep stepping until you reach
```
long first = fib(n - 2);
```
Step into that call again. And keep clicking on the “Step Into” button. Watch the call stack (Window -> Debugging -> Call stack) and the variable display (Window -> Debugging -> Variables). Describe what you see. What is n? What is on the call stack?
Not surprisingly, when you debug a recursive method, you can observe that the method calls itself multiple times.
It would be pretty tedious to keep stepping in all the way to the base case, so set a break point on line 27 and click the Continue button

How many invocations of fib are on the run time stack now?
Remove the breakpoint on the return 1 line and set a breakpoint at the line
```
long result = first + second;
```
Click the Continue button (or hit the F5 key). What is the value of n? What is the value that is about to be returned? (You may need to click on the Variables tab to see the values of n, first, and second.)
Click Continue a few more times. Write down the values of n, first, and second, that you encounter. Do this for at least ten values.
Now look at the values that you recorded. What do you notice? Why does that explain that the method runs so slowly?

E. Logging

In the previous section, you saw how to use the debugger for analyzing, and that is often the best strategy. It is, however, not the strategy that students use most commonly. Inexperienced programmers often sprinkle their code with print statements like these:

System.out.println("Yoohoo! I got this far!");
System.out.println(n);

Print statements can waste a lot of your time. You put them in, you take them out, you put them back in, you comment them out, you remove the comments, and when it all works you take them out for good. Until the next bug appears and you wish you had left them in.

In this section, you will practice the use of logging statements. Logging is easy. Instead of System.out.println, simply use Logger.getGlobal().info. For example,

Logger.getGlobal().info("Entering fib. n=" + n);

Logging is better than System.out.println for two reasons:

There is no shame in logging. You can leave the logging statements in your code when you turn it in, demonstrating good software engineering practice.
It is easy to turn all logging statements on or off.

Logging can be better than using the debugger.

The price of entry is much lower. It is very easy to add a logging statement, but it takes some effort to start a debugger session.
With logging, you have a complete record of what happens (provided, of course, you inserted enough statements to have a complete record). With a debugger, you only have that if you diligently wrote your observations into your notebook.

Let's try this with the fib method. At appropriate places, add the following logging statements:
```
Logger.getGlobal().info("Entering fib. n=" + n);;
```
```
Logger.getGlobal().info("Exiting fib. return=" + ...);;
```
What is the code for your fib method?
In the main method, add
```
Logger.getGlobal().setLevel(Level.ALL);
```
Run your program (changing the upper limit of the loop in the main method to a small enough value). What is the output?
How does the output demonstrate the inefficiency of the method?
One way of making the method more efficient is to use a technique called memoization. Remember previously computed results and don't recompute them. Add a static array knownFibonacciValues to the class. In the fib method, first look up knownFibonacciValues[n]. If it is non-zero, return it. Otherwise, compute it in the normal way. Just before returning, call knownFibonacciValues[n] = return value so that it is know the next time.
What is the code of your method?
What is the logging output now?
What happens when you try again with n = 50?
Now change the setLevel call of the main method to
```
Logger.getGlobal().setLevel(Level.OFF);
```
Run your program again. What happens?
That is the power of logging. You can deactivate the messages without having to remove them.
Suppose you find another bug and want to turn logging back on. How do you do that?

In a small program, using Logger.getGlobal().info works fine. As your programs grow larger, you can control your logging in more sophisticated ways. You can use different logging levels. Instead of info, call methods severe for important messages or fine for "fine-grained" messages. Then call the setLevel method to set the level of the messages that you want to see in a particular program run. You can also define your own logger objects in addition to Logger.global. Keep this in the back of your mind; it will come in handy in the future.